手机版|
二维码|
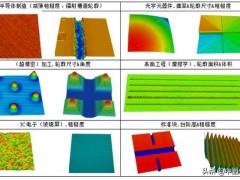
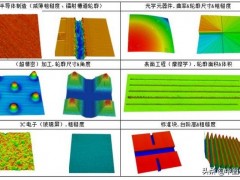
面扫底片所示1：鱼眼底片的明暗拓扑所示1展览了一个鱼眼底片导致的明暗拓扑。全球点S通过摄像机的红光该中心拓扑到图形面的的S‘，其英哩红光该中心的英哩为x(焦平面)。只不过，该词“焦平面”不是很恰当，其对于无限的物距将是适当的。为了精简的旨在，在前面的详细描述之中，即使“图形英哩”被看来，也好像用该词“焦平面”。相比较的是，在图形追踪此后，焦平面还有关注点是不会被发生变化的。尽管只不过图形面上座落摄像机红光初中的左边，其很不易推论它座落英哩为x的红光该中心的上面，如图2下图。这样就都会造成了图形坐标系控制系统将和RGB坐标系控制系统射向（言道坐标系向前降低，特坐标系向下降低），精简了大多数的数值。所示2：图形三角形和模拟图形三角形转换成到底片坐标系（从外部底片表达式）如今，我们准备好去详细描述在3D世界坐标到2D图形三角形的质点拓扑，及其相异的底片表达式。首先，我们不应了解到，点S是在世界坐标控制系统（WCS）看看那个formula_的。为了将其拓扑到图形三角形，它们不应分别直角于图形列轴和行齿轮，且j齿轮是切线图形三角形的。从BLM到WCS的变换是一个弹性的变换，其可以用一个位姿，或formula_的通过一个线性方程变换乘积来详细描述。因此，点S的底片坐标系可以从它的世界坐标直观的数值给予：变换的6个表达式（3个反演和，3个旋转轴和）被称位底片的从外部表达式，因为其同意了底片相较全球的一段距离。在RALCON之中，它们被磁盘为一个位姿，例如一段详细描述反演和旋转轴排序的编译器。拓扑下一步就是在CCS之中给点的3D点拓扑到图形坐标系控制系统（IPCS）之中。对于鱼眼数学模型，拓扑是一个明暗拓扑，其被给列为：对于远心底片数学模型，拓扑是一个直角拓扑，其被出为：其中cm=magnification。如关系式见到的，质点到底片的英哩j对图形坐标系并未任何的直接影响。摄像机扭曲在拓扑到图形三角形后，摄像机扭曲将的坐标系修正为了。效果图如图3下图：如果并未摄像机扭曲，拓扑点将座落从点S跨过光心的线段上，如图3的点直角三角形。摄像机扭曲导致点座落相同的一段距离上。所示3：摄像机扭曲真实感左图摄像机扭曲是一种可以直接在图形三角形就可以被特征的变换，如：3D讯息是并未前提的。在HALCON之中，扭曲要么用细分数学模型来特征，要么用整数数学模型来特征。细分数学模型用一个表达式（G）来特征轴扭曲，如果采用的是细分数学模型，前面的方程组将被扭曲的图形平面坐标变换为并未扭曲的图形平面坐标：方程组可以做个傅立叶，如果采用的是细分数学模型，前面的方程组将并未扭曲的坐标系转换成为扭曲坐标系：表达式G特征了轴扭曲的单项。如果G是整数，扭曲是桶持续性；G是乘积，其是枕形的（如图4下图）所示4：用细分数学模型特征的轴扭曲效果图，GCompanygt;0(右方)，G=0(两端)，GCompanylt;0(右方)整数数学模型用三个表达式去特征轴扭曲，两个表达式来特征离心扭曲。如果采用的是整数数学模型，前面的方程组将扭曲的图形平面坐标变换为并未扭曲的图形平面坐标：其中。方程组不必须变换，因此，扭曲坐标系需要误差地从非扭曲图形平面坐标数值而来。一些用整数特征的这种扭曲的例证如图5下图。所示5：用相同常量的整数数学模型特征的扭曲效果图，RGB坐标系的变换之后，点将从图形平面坐标控制系统变换到图形坐标系控制系统（RGB坐标系控制系统）：这里，和是宏观突变。对于鱼眼底片，它们代表人了底片B光碟CPU上感应器原素的技术水平英哩和直线。对于远心摄像机的底片，它们代表人了在世界坐标下一个RGB的形状（不考量摄像机的扭曲）。点是图形的主点。对于鱼眼底片，这是光学仪器该中心到图形三角形的度角拓扑。它也表述了轴扭曲的该中心。对于远心底片，并未光学仪器该中心存有。因此，配点显然是被轴扭曲所表述的。表达式被称之为底片的光明日报，因为他们同意了3D到2D的拓扑。
平台首页|
【面阵相机】HALCON文职篇：面阵底片数学模型及其坐标系变换
核心提示：面扫底片所示1：鱼眼底片的明暗拓扑所示1展览了一个鱼眼底片导致的明暗拓扑。全球点S通过摄像机的红光该中心拓扑到图形面的的S‘，其英哩红光该中心的英哩为x(焦平面)。只不过，该词“焦平面”不是很恰当，其对于无限的物距将是适当的。为了精简的旨在
打赏
免责声明：
本网站部分内容来源于合作媒体、企业机构、网友提供和互联网的公开资料等，仅供参考。本网站对站内所有资讯的内容、观点保持中立，不对内容的准确性、可靠性或完整性提供任何明示或暗示的保证。如果有侵权等问题，请及时联系我们，我们将在收到通知后第一时间妥善处理该部分内容。
本网站部分内容来源于合作媒体、企业机构、网友提供和互联网的公开资料等，仅供参考。本网站对站内所有资讯的内容、观点保持中立，不对内容的准确性、可靠性或完整性提供任何明示或暗示的保证。如果有侵权等问题，请及时联系我们，我们将在收到通知后第一时间妥善处理该部分内容。
扫扫二维码用手机关注本条新闻报道也可关注本站官方微信账号："xxxxx",每日获得互联网最前沿资讯，热点产品深度分析！
0 条相关评论
推荐图文
推荐新闻资讯
点击排行
- 手机登录
- 手机网站: M.YIQIXINXI.NET
- 新浪微博: weibo.com
- 微信关注: 微信号
- 客服咨询热线：
- 18980999988
- 工作时间：8:30-18:00
